Many scientists consider the search for related work as an extremely time-consuming part of their responsibilities. The enormity of time taken is partly caused bythe increasing number of publications, which grows exponentially at a yearly rate of 3.7%. Instead of entering just keywords, a user may provide entire documents, including reference lists as input and make implicit and explicit ratings to improve recommendations. Instead of solely relying on text mining, recommender system could combines citation analysis, implicit ratings, explicit ratings, author analysis and source analysis to a recommender articles to the users. For more details look at this paper.
Recommender system is designed to predict the user preference and how to recommend the right items in order to create a user personalization experience. There are two types of recommender system: 1 - Content based filtering: focused on the similarity attributes of the items to give recommendations. 2 - Collaborative filtering: focused on the similarity attribute of the users finding people with similar tastes based on a similarity measure: memory based and model based.
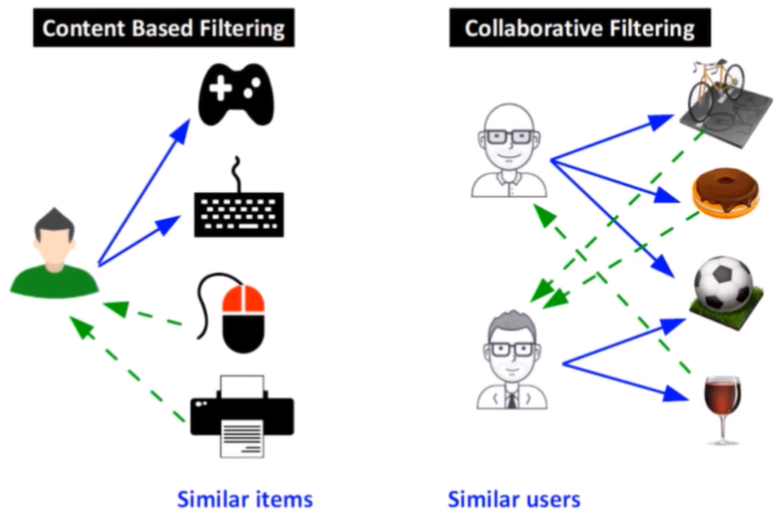
From the figure above, the content based filtering is able to find similar items of the favorite items of the user, such as the mouse and the printer based on the keybord and the joystick. The recommendation is based on the similarity. On the contrary, in the collaborative filtering is focused on the similarity attributes of the users, finding peole with similar traits based on a similarity measure. There are two measures: memory based and model based.
The memory based recommendation is looking items liked by similar people in order to create a ranked list of recommendations. We can sort the ranked list to recommend the top n items to the user. The Person correlation and cosine similarity are used. Here the Pearson correlation formula:
\[ \operatorname{simil}(x, y)=\frac{\sum_{i \in I_{y}}\left(r_{z, i}-\bar{r}_{z}\right)\left(r_{y, i}-\bar{r}_{y}\right)}{\sqrt{\sum_{i \in I_{y}}\left(r_{z, i}-\bar{r}_{z}\right)^{2}} \sqrt{\sum_{i \in I_{y}, i}}\left(r_{y, i}-\bar{r}_{y}\right)^{2}} \]
and the cosine similarity formula:
\[ \operatorname{simil}(z, y)=\cos (\vec{x}, \vec{y})=\frac{\vec{x} \cdot \vec{y}}{|\vec{x}||\times| \vec{y}||}=\frac{\sum_{i \in I_{y}} r_{z, i} r_{y, i}}{\sqrt{\sum_{i \in l_{z}} r_{z, i}^{2}} \sqrt{\sum_{i \in l_{y}} r_{y, i}^{2}}} \]
The cosine similiarity formula (see on top of this article) makes sure how to separate two terms where each term is represented by a vector and we are interested in the angle between these two vectors. If the cosine similarity is close to 1, both terms are very similar. In the memory based recommendation the similarity matrix is used.
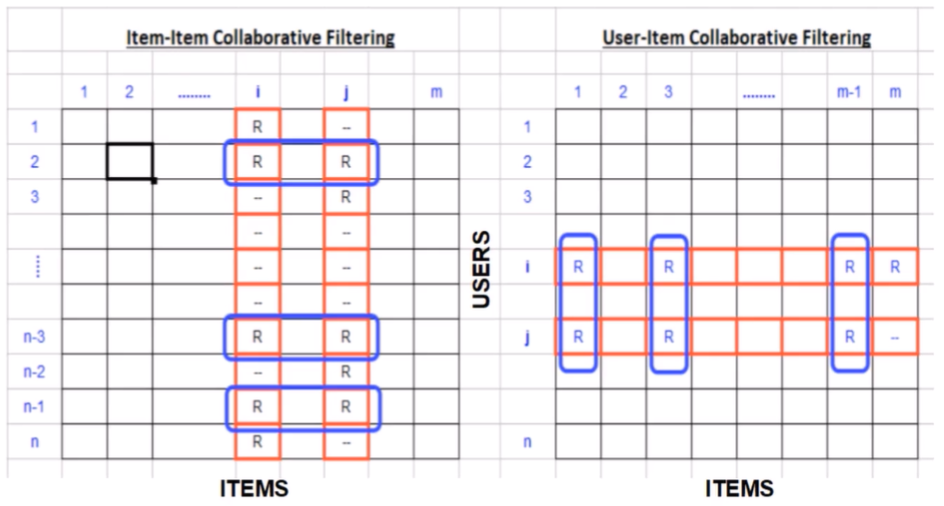
From the figure above we can see on the left the item-item similarity which is calculated by looking into co-ranked items only. Form example, for the items i and j the similarity is computed by calculating similarity between rating the i and j columns (items) but only in the cells where we have a rate (blue rectangles). Another approach is to use the user-item similarity, on the right of the figure above. This approach is looking into correlated items only in rows (users).
A pratical application is about scientific publications. The amount of digital text data is growing exponentially and it is time consuming for researchers to find relevant information and the researched more connected to the same area of research. We can use the following variabels: 1 - user: the name of researchers 2 - topics: the specific area of research 3 - cites: number of quotes received by an article 4 - date: date of publication used as a cut-off to split the data between train and test set
Having there variables we can implement a ANN to find attribute of the users finding researchers with similar influence on a specific topic based on a the number of quotes (collaborative filtering). We can also try to use a more simple approach: content based filtering.
Content based filtering applied to scientific publications Content based filtering focused on the similarity attributes of the items to give recommendations. The content based filtering recommend items (scientific articles) based on the attributes of those items themselves. The figure below is an example of the cosine similarity to find similar articles.
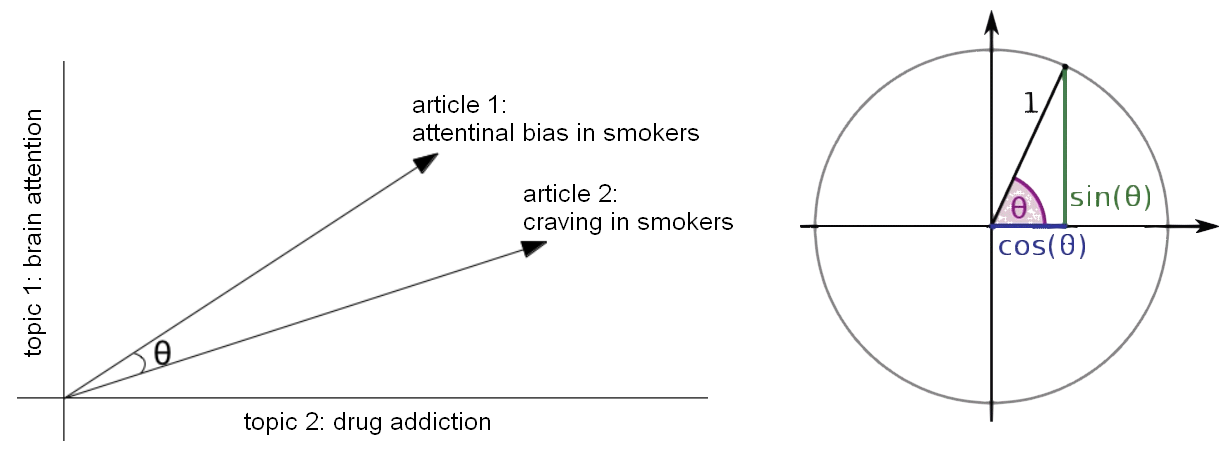
The article 1 (attentional bias in smokers) has a theta angle of 45 degree and this corrispond to a similarity of 0.7. This means that the article 1 is related to both the topic brain attention mechanisms and drug addiction. Bolow the formula to calculate the cosine similarity in amultidimentional space.
\[ \operatorname{cossim}(x, y)=\frac{\sum_{i} x_{i} y_{i}}{\sqrt{\sum_{i} x_{i}^{2}} \sqrt{\sum_{i} y_{i}^{2}}} \]
The x and y in the formula above are topic1 and topic2 respectively. By taking the summation of each topic x and y and dividing by the square root of the summations squared, we end up with the cosine similarity score. We can also take in consideration the date of publication of the articles. The idea is that how far apart would two movies have to be for their date of publication, signify that they are sunstantially different. A decade shoudl be a reasonable starting point (e.g. an article about brain activity in the 80s are different the same article in the 90s). We can use the code below to scale the difference in dates from zero to one.
def computeYearSimilarity(self, topic1, topic2, years):
diff = abs(years[topic1] - years[topic2])
sim = math.exp(-diff / 10.0)
return sim
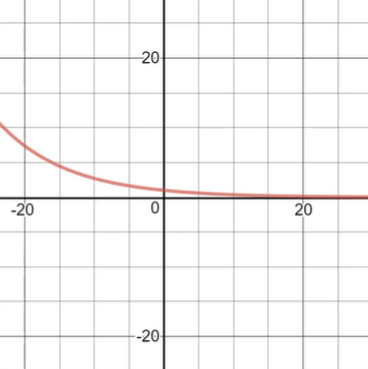
From the code above we can see the exponential decay function is used. The similarity socre decays exponentially which is relly small after 10 years and almost nothing after 20 years as we can see from the figure below.
In the real world we can use test many variatins of this function to see what really produces the best recommendations with real articles. To predict a rating for a given researcher and for a given topic can be made using a k nearest neighbors. The idea is to measure the similarity score between the article and all other article rates (e.g. number of cites). In this case nearest neighbors are the articles with the highest content-based similarity scores, and we can use the top 10 nearest articles to recommend to the users.
Collaborative filtering applied to scientific publications Collaborative filtering focused on the similarity attribute of the users finding people with similar tastes based on a similarity measure.

In the figure above, we can see that we have the rating information (e.g. number of cites) made by other authors. We can also looking up other topics similar to the user topic to find our finat top recommended articles. A key role is played by the item similarity or similar users.

From the table abov, we can see that we could have sparcity problem. Thayt is why collaborative filtering works well when we have large amount of data. Sparsity also introduces some computational challenges. In fact, we don’t want to store and processing missing data and sparse arrays are used to avoid empty space in the matrix. This remind us ther quantity and quality of the data it is often more important than the algorithm that we use.
Similarity Metrics There is aprobem in scientific publicatioin which is related to the impact factor of the journal. In fact, there are journals such as Nature tha has a very high impact factor but that is due to the fact that it is multidisciplinary. On the contrary, other journal are more focus on a specific area of research, and as a consequence they have lower impact factor even if they have many readers. Therefore, we have different baseline for different journals. The adjusted cosine attempts to normalize these differences.
\[ \operatorname{cossim}(x, y)=\frac{\sum_{i}\left(\left(x_{i}-\bar{x}\right)\left(y_{i}-\bar{y}\right)\right)}{\sqrt{\sum_{i}\left(x_{i}-\bar{x}\right)^{2}} \sqrt{\sum_{i}\left(y_{i}-\bar{y}\right)^{2}}} \]
From the furmula above, we can use x average and y average as the impact factor devided by the number of area of research the the journal contains. A slight twist on adjusted cosine is the pearson similarity; it looks at the difference between number of cites of an author and the average of cite of an article. We can think of person similarity as measuring the similarity between authors by how much they diverge from the topic rate.