The Word2Vec is a semantic learning framework that used a neural network to learn the representation of words or phrases in a text. It is usefull to understand the semantic meaning behind a term. This algorithm use two methods: 1 - CBOW 2 - SkipGram In Continuous bag of words CBOW predicts the current word from a window of surrounding context words, or given a set of context words predicts the missing word that is likely to appear in that context. The SkipGram predicts the surrounding window of context words using the current word of given a single word, predicts the probability of other words that are likely to appear near in tat context. SkipGram is known to show good results for both frequent and rare words. This process is similar to the NGram but now the window is applied also to the preavious words of the input word; the neuranl network is able to learn the combination between both preaviuos and posteriors words in a semantic way.
The Word2Vec is a deep learning algorithm that draws context from phrases. Every textual document is represented in the form of a vector, and that is done through Vector Space Modelling (VSM). We can convert our text using One Hot Encoding. For example, having three words we can make a vector in a three dimentional space.
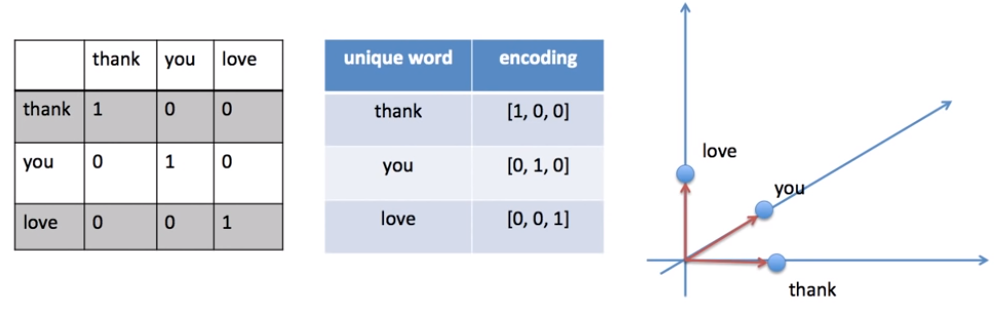
The problem with One Hot Encoding is that it doesn’t help us to find similarities. In fact, from the graph above, every distance is same from each other, and we cannot find similarities using for example Euclidian Distance. That is why Word2Vec data generatiioin also known as Skipgram is used. The Word2Vec is a Word Embedding where similarities come from neighbor words.
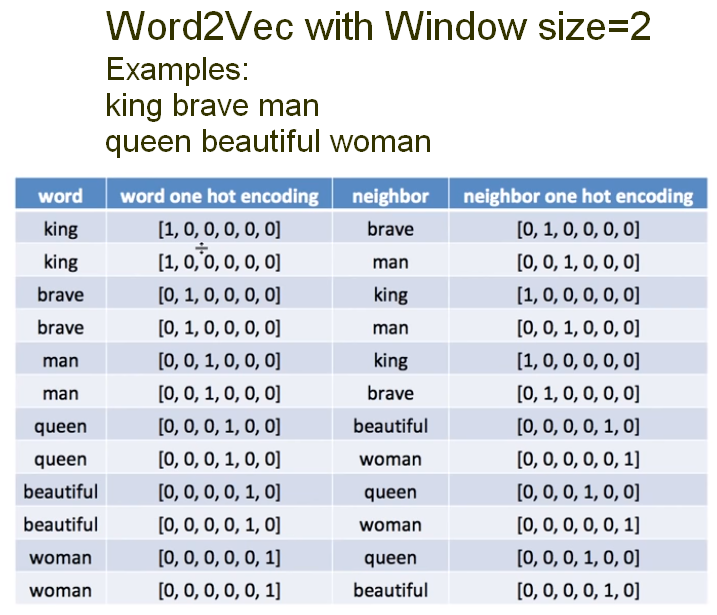
From the example above, we converted the words in a One Hot Encoding, and we also codified the Neighbor One Hot Encoding. The architecture of the Word2Vec is as described below.
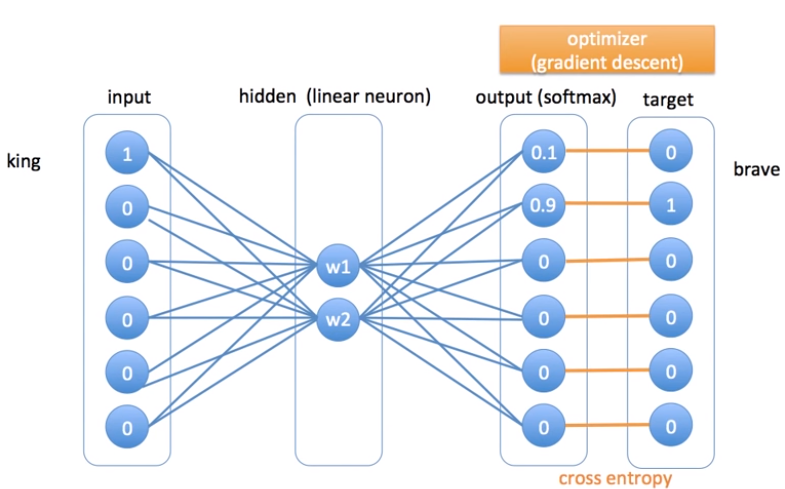
The example described by the figure above, try to train the word king as input and brave as neighbor using gradient descent as optimizer. During Backpropagation we have an update of the Weights in the Hidden layer for each combination of words, and the inputs are multiplied with the updated weights. The Weights continue to be aìupdated during each combination of words based on the context of each phrase. The Softmax Function create the probability distribution, and Gradient Descent is used as optimizer. There is an interesting simulation here where we can simulate to train a ANN and see how it developes.
The crucial point is to be able to predict the Context Word from the Focus Word, namely the word in the sentence.
\[ \log p(c | w ; \theta)=\frac{\exp v_{c} \cdot v_{w}}{\sum_{c^{\prime} \in C} \exp v_{c^{\prime}} \cdot v_{w}} \]
From the function above, we are going to take the probability of the context word given the focus word as the product between the contex word vc and the focus word vw. The formula remind us the Sigmoid Function of the Logistic Regression. One important detail of Word2Vec is related to the distributioin of the probability of the context word. In fact, the robability of words is typically raise to the power of 3/4 called Negative Sampling Distributin.
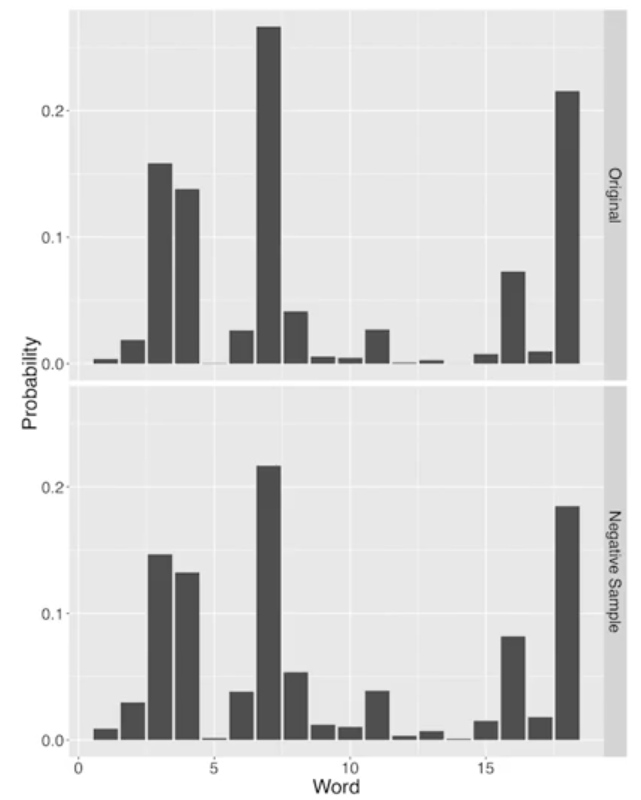
As we can see from the figure above, raising to the power of 3/4 is able to bring down frequent terms, and bring up infrequent terms. As a result, we are focusing only on super frequent words, but also we are considering words that are in the middle range of our distribution and we can explore more at the long tail of the distribution. The Negative Sampling Distribution with a power of 3/4 makes the distribution a little bit fatter and longer.
There is an interesting simulation here where we can simulate to train an ANN and see how it develops. And here the related theory.