This article is a summary of the StatQuest video made by Josh Starmer. Click here to see the video on K-Mean explained by Josh Starmer. Click here to see the video on Hierarchical Clustering explained by Josh Starmer.
Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). Cluster analysis itself is not one specific algorithm, but the general task to be solved. It can be achieved by various algorithms that differ significantly in their understanding of what constitutes a cluster and how to efficiently find them.
K-Means Clustering The main question in K-Means Clustering is: can we identify certain groups among all variables? The STEP 1 is to identify the number of clusters K. Suppose we have K=3, the STEP 2 is to select randomly 3 data points, and these are our Initial Cluster Points. The STEP 3 consists to calculate the Euclidian Distance between the observations and the Initial Cluster Points.
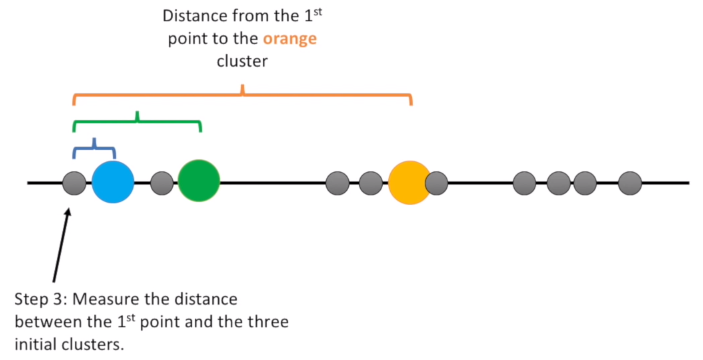
The STEP 4 consist to assign the observations to the nearest cluster. Then, the STEP 5 calculate the average of each cluster. Now, we have to asses the right cluster by adding-up the variation within each cluster. We don’t know the best clustering, and so we can only try again to select randomly the initial cluster points and compare the variation with the previous attempt. And we do this over again with different starting point.
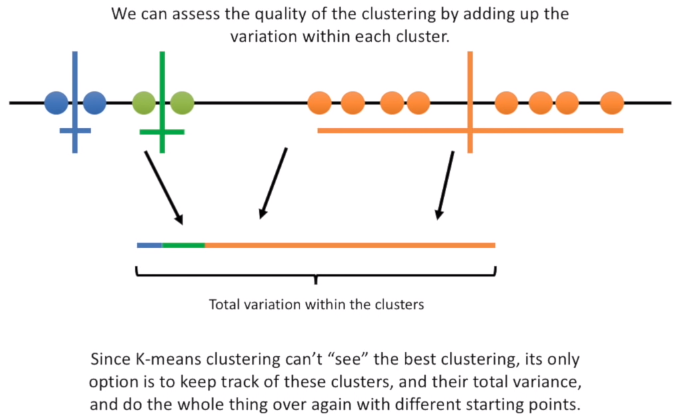
With this approach, we can find the best Initial Cluster Point that have the lowest variation, but we still we don’t know if that variation is the lowest overall. To solve this question, could be very useful to find a method to identify the Best Number of K. The Elbow Plot helps us to find when the variation is stabilized based on the number of K.
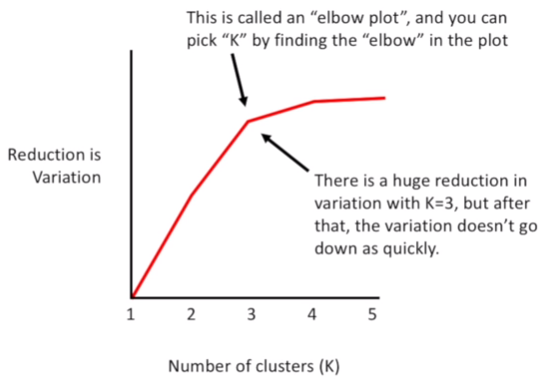
Essentially, each time we add a new cluster, the total variation within each cluster is smaller than before. The goal is to stop the number of K when the variation stops to decrease, that is why is called elbow.
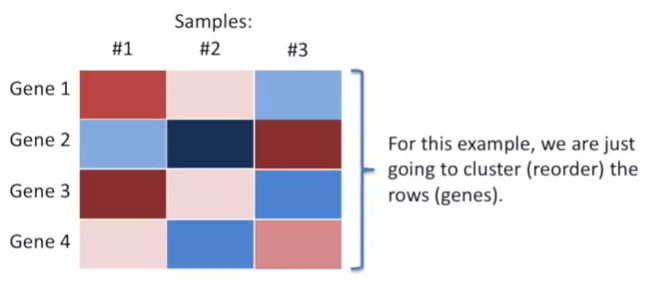
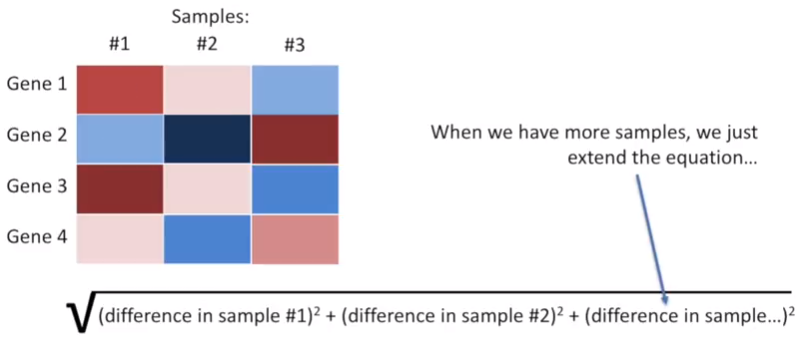
Hierarchical Clustering It always refers to heatmap plot. The columns represent different samples, rows represent measurements from different variables. The Hierarchical Clustering orders the rows and the columns based on similarity. This makes it easy to see correlations in the data. Heatmaps often come with dendrograms that indicates the similarity and the cluster of membership. Cluster with more similarity have shorter dendrogram branch as we can see from the fgure below.
The defined method for determining Similarity is the Euclidean Distance between Observations, we can also use the Manhattan Distance that is the absolute value of the differences.
Now, to assign new observations to a cluster based on the Center Point, we have to explore all the possible methods that are: Centroid: the average of each cluster. Single-Linkage: the closest point in each cluster. Complete-Linkage: the furthest point in each cluster. The ultimate goal is to find the best method able to gives more insight into our data.
Summarizing, in Hierarchical Clustering clusters are formed based on some notion of similarity, and we have to decide what that is. However, most programs have reasonable degaults. Once we have a sub-cluster, we have to decide how it should be compared to other sub-cluster.