The Social Network Analysis is simply a set of objects, which we call nodes, that have some relationships between each other, which we call edges. The first reason to study networks, is because networks are everywhere. In social networks the nodes are people, and the connections between the nodes represent some type relationship between the people in the network. There are many metrics to estimate the importance or better, the centrality od a node in a network such as Closeness centrality and Betweenness centrality. The page rank was developed by the Google founders when they were thinking about how to measure the importance of webpages using the hyperlink network structure of the web. And the basic idea, is that PageRank will assign a score of importance to every single node. And the assumption that it makes, is that important nodes are those that have many in-links from important pages or important other nodes.
The Page Rank can be also used on any type of network, for example, the web or social networks, but it really works better for networks that have directed edges. In fact, the important pages are those that have many in-links from more important pages.
How it works At first, we start with every node having a PageRank value of 1/n. And then what we give all of its PageRank to all the nodes that it points to, and then we do this over and over again performing these Basic PageRank Updating Rules k times. And then, the new value of PageRank for every node is going to be simply the sum of all the PageRank that are received from all the nodes that point to it.
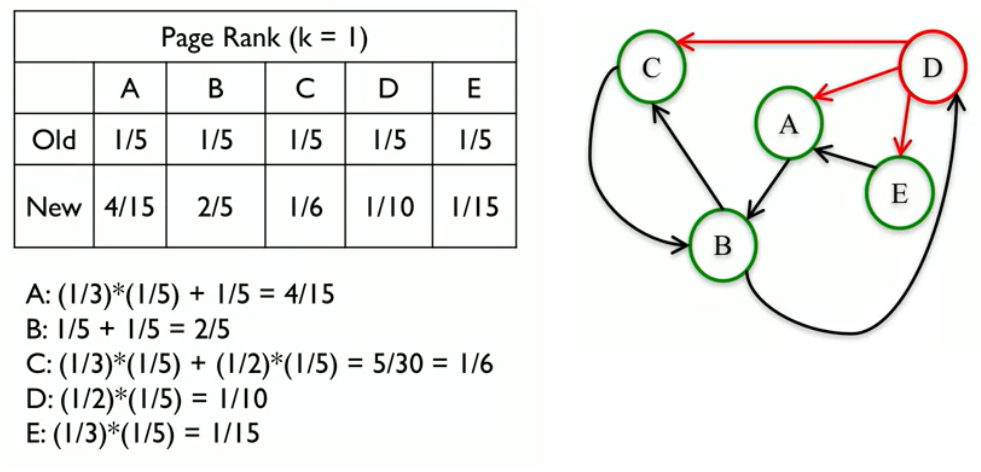
At this point, we assign every node a PageRank of 1/n. Looking at the figure above, every node will have a PageRank value of 1/5. And now we’re going to start applying the Update Rule. So we’re going to have to keep track of the old values of PageRank, and what the new value of PageRank of each node is. Let’s start with node A. Nodes D and E point to node A, so A is going to get PageRank from D and E. Now let’s think about how much PageRank A is going to receive from each one of those two nodes. So if we look at D, D has three edges, that points to three different nodes, C, A, and E. So A is going to receive 1/3 of the current page rank that D has. D currently has 1/ 5 PageRank, and so A is going to get 1/3 of that 1/5 PageRank that D has. Now A is also going to get PageRank from node E, and because E only points to A, then it’s going to give all of its PageRank to node A. And so A is going to get 1/5 PageRank from node E. And so, in total, A is going to get 4/15 PageRank from those two nodes. And so the new value PageRank of node A is 4/15. Now, let’s think of node B. We use the same approach for each nodes on the network. The figure above represents the PageRank at Step 1.
Crucially, we do the exact same thing again to get the second step of PageRank, k equals 2 in order to obtain the PageRank at Step 2 as shown in the figure below.
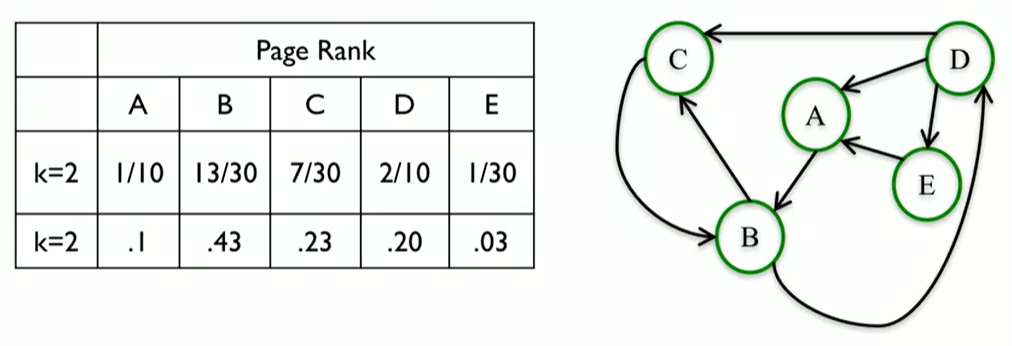
From the figure above, after two steps we find that node B has the highest PageRank (0.43), followed by node C, then node D, node A, and E. This point, this is suggesting that B is the most important node in this network. What happens if we continue for another step? If we continue with more steps we might notice that the values change a little bit, but they still have the same order and B is sitll the highest PageRank node.
Scaled PageRank The PageRank value of a node after k steps can be interpreted as the probability that a random walker lands on that node after taking k random steps. Random walk means we would start on a random node, and then we choose outgoing edges at random, and follow those edges to the next node. And then you’re going to repeat this k times. We simply randomly choose edges and walk along in the network and the value of PageRank of each node is the probability that you would land on that node after k steps. If you repeat this for a lot of steps, say k equals infinity. These are the values that you can eventually approach, these are the values that you converges to.
Lets make a small change to this network adding two nodes, F and G, where B points to both of those nodes, and then they point to each other as depicted in the figure below.
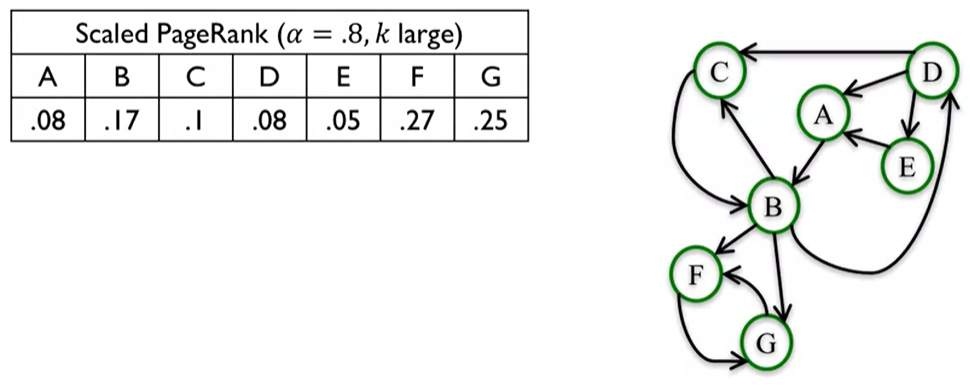
We want you to look at this network and try and figure out what the PageRank of each node is after taking a lot of PageRank steps for example 4k. For large enough k, F and G are going to have a PageRank value of about one half. And all the other nodes are going to have a PageRank value of 0. That is due to the fact that whenever the random walk lands on F or G, then they’re going to stock on F and G because there are no edges to go to. There is no way to get back from G and F to any of the other notes. The way we fix this problem is by introducing a new parameter to the PageRank computation called this damping parameter alpha and we make the random woalk with the with probability 1- alpha and by doing this we get unstuck whenever we actually choose a random node. Crucially, for most networks as k gets larger, the Scaled PageRank converges to a unique value. Using Scaled PageRank now we have F and G still with a very high PageRank compared to the other notes. But the other nodes don’t have a PageRank value of zero. It is important to note that this damping parameter works better for large networks like the web or very large social networks.
Reference: Appied Social Network Analysis