Supposing we are implementing a mini-batch gradient descent of just 64 or 128 examples. During the interation we can occur to the problem to not converge to the minimum. That is expecially true when we use fixed values of alpha learning rate. On the contrary, when we slowly reduce the learning rate alpha we are able to end up oscillating in the region around the minimum.
First, we have to remember that one epoch is one pass through the training set.
\[ \alpha=\frac{1}{1+d_{\text {decay-rate}} * \text { epoch-num }} \alpha_{0} \] Where decay-rate is an hyperparameter that we need to tune, and apha0 is the initial learning rate. If we start with a alha0=0.2 and a decay-rate=1 and using the formula above, then the alpha tends to decrease over the epochs. So, to use learning rate decay we can try a variety of both hyperparameters alpha0 and decay-rate. We can also use other method: 1 - the so called exponential decay where alpha is some numbers less than 1. The calculation is: aipha=0.95^epoch-num * alpha0 2 - there is also the discrete stair-case. The calculation is: alpha=k/sqrt(epoch-num) * alpha0 3 - some people also use the manual decay. Here we just check the time for training our model and we stop if the process is too long. At this point, we manually descease the alpha hyperparameter to speed up the process. Of course, this is feasible only if we are dealing with a small training-set.
The problem of local optima Looking at the figure here below on the left, it is quite common to get stuck to a local minimum rather than find the way to a global optimum. In reality, most of the points of zero gradient are not local optima like in the figure on the left, but instead most points of zero gradient are in a so called saddle points as pictured on the right figure.
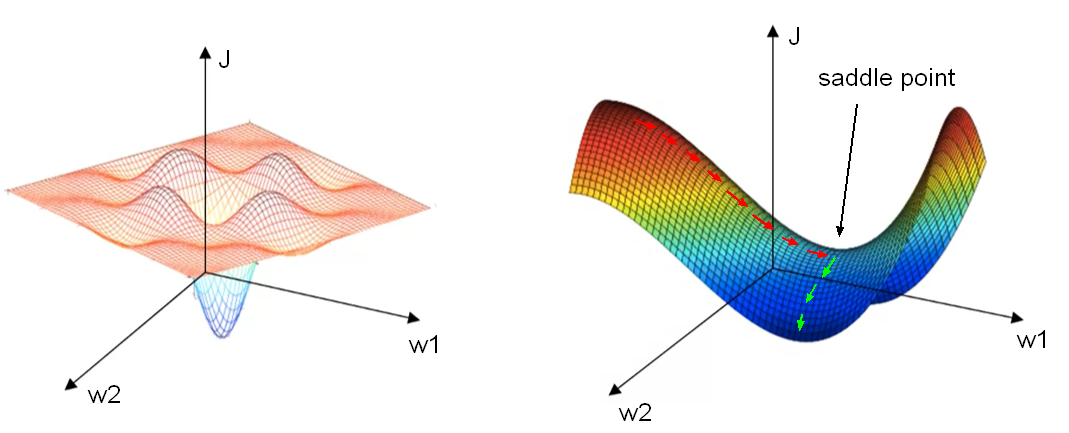
The saddle point has derivatives equal to zero and we have the Problem of Plateaus which is a region where the derivative is close to zero foor a long time. The Plateau can really slow down the learnind. The plateau is represented by the red arrow on the right figure. In fact, the process takes long time before realize to follow the green path in order to reach the minimum. This is the scenario where more sophisticated observation algorithms, such as AdaM, can actually speed up the learning-rate.
Reference: coursera deep neural network course