This article is a summary of the StatQuest video made by Josh Starmer. Click here to see the video explained by Josh Starmer.
Locally weighted regression scatterplot smoothing - LOWESS The main idea to fit a curve to data point is to use a type of sliding window to divide the data into smaller blobs. The second main idea is that each data point use the least squares to fit a line.
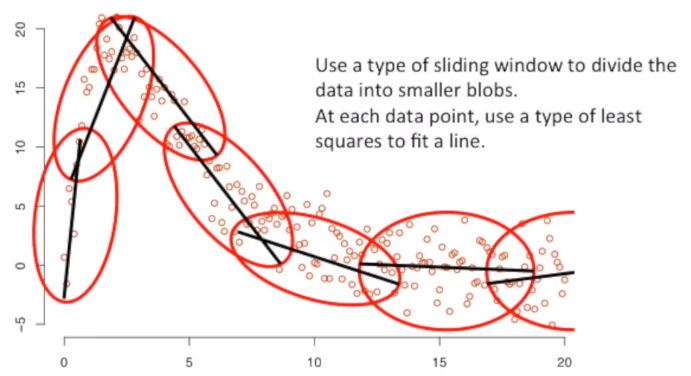
Let’s say we start with a sliding window of 5 observations. The first observation of the sliding window is called Focal Point. We perform a Weighted Least Squares on all the 5 points. The closer the point is to the Focal Point, the more weight (or influence) it has on determining the fit of the line.
One option for non-linear regression is to fit a Polynomial Model (e.g. Y = β0 + β1X + β2X2). These are superficially attractive, because higher order polynomials can be made to ‘fit’ almost any pattern. However, interpretation of such models is very difficult and their shape is sensitive to outliers. LOWESS regression is often a preferable approach.
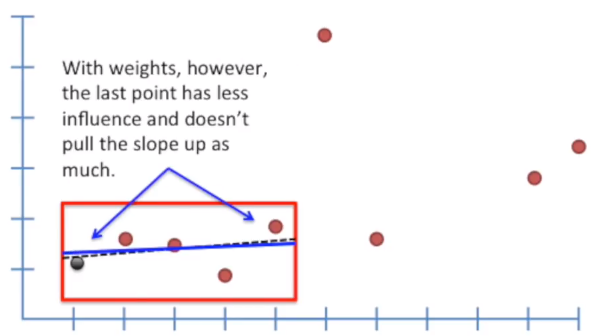
Using weights, the last point has less influence and doesn’t pull the slope up as much. Now, we use the same sliding window, but we use the second observation as a Focal Point, and again we perform the weighted least squares using the second point as Focal Point. We continue this process for all the 5 point considered in the sliding window.
To reduce the influence of outliers we also introduce a second weight that is based on the how much the points are close together along the y-axis: the more they are, the more the weight.
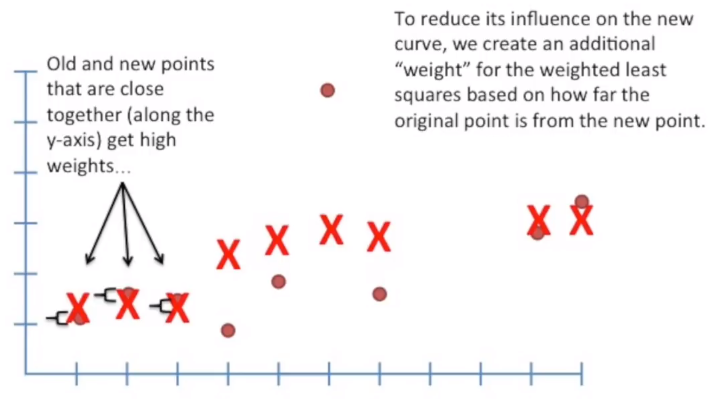
After the adjustment based on the similarity of variance on the y-axis, we typically have a smooth curve.
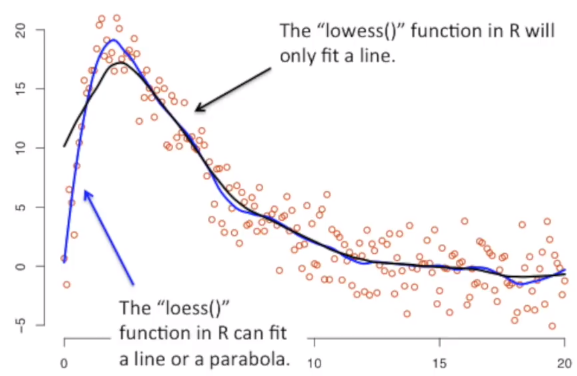
We can decide to use a line or a parabola to fit the data. The loess function will fit only a line. The lowess (locally weighted scatterplot smoothing) function will fit a parabola. The lowess function allows to draw confidence intervals aroud the curve. We can also change the window size to contain more or fewer points. But instead of specifying the exact number of points, we usually specify the proportion of the total.