This article is a summary of the StatQuest video made by Josh Starmer. Click here to see the video explained by Josh Starmer.
In Gradient Descent, we used the sum of the squared residuals as the Loss Function to determine how well the initial line fit the data. Than, we took the derivative of the sum of the squared residuals with respect to the intercept and slope. We repeated that process a lot of times untill we took the maximum number of steps, or the spteps became very, very small.
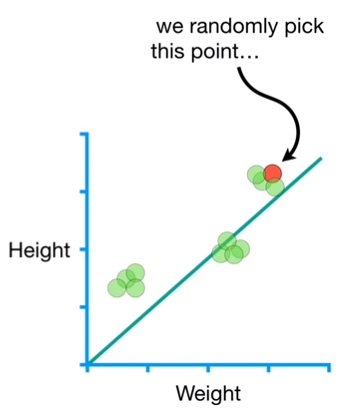
Now, imag to have a Logistic Regression that used 10000 genes to predict if someone will have a disease. This means, we would have 10000 derivatives to plug the data into. so, for Big Data, Gradient Descent is too slow. This is where Stochastic Gradient Descent comes in handy. If we have 10000 samples, than Stochastic Gradient Descent would reduce the amount terms computed by a factor of 10000. It is specially iseful when there are redundancies in the data. For example, if we have 12 data points that form 3 clusters. We start by picking a point randomly and we calculate the Height and Weight as presented in the example below.
Just like with regular Gradient Descent, Stochastic Gradient Descent is sensitive to the value we choose for the Learning Rate, and again, the general strategy is to start with a relatively large Learning Rate and make it smaller with each step. The way the Learning Rate changes, from relatively large to relatively small, is called the Schedule.
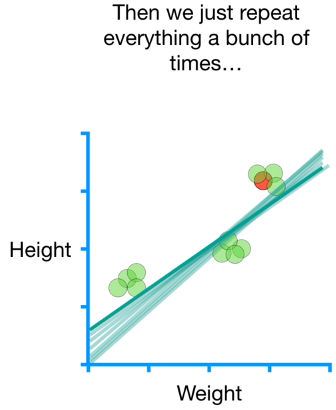
We reapeat the calculatetion of intercept and slope, moltiply by the Learning Rate for each point picked at random.
Note that the strict definition of Stochastic Gradient Descent is to only use one random point per step. However, it is more common to selec a small subset of data, or the so called mini-batch, for each step.
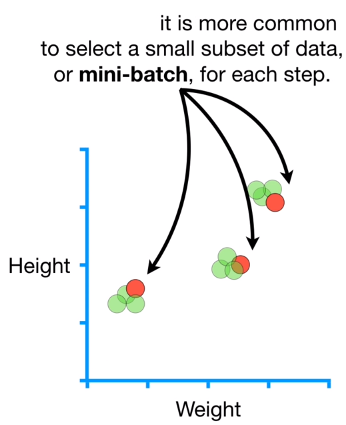
Using a mini-batch for each step takes the best of both world between using just one sample and all of the data at each step. Similar to using all of the data, using the mini-batch can result in more stable estimates of the parameters in fewer steps, and is much faster than using all of the data in one single batch also called the gold standard. So, just using for example 10 sample point per step, we can ended up closer to the gold standard. One cool thing about Stochastic Gradient Descent is that when we get new data we can easly use it to take another step for th parameter estimates without having to start from scratch.
Summarizing, Stochastic Gradient Descent is great when we have tons of data and a lot of parameters. In these situations, regular Gradient Descent may not be computationally feasible.